MatLab 2, Thermal Systems Part 1

Deliverables:
Questions 1&2, the .m files and resultant graphs for the four temperature controllers assigned on page 9, and your responses to the questions about those controllers.

Question 1 How does the cooling behavior change if we vary the parameters Rth and C? Figure this out using intuition and the above equations, and then vary these parameters in your program to confirm your conclusions.

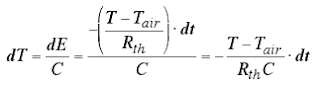
As Rth and C increase, dT will decrease. This means that the higher the Rth value and/or the C value are, the slower the coffer will cool.

Red circles = Rth, cyan=  C

Question 2 Calculate a good value for P if we want our coffee to heat up to the
Starbucks ideal 84°C?

P is the value of the thermal energy provided by the heater. Our coffee begins at 84°C (357K) and we want it to stay there. So what we want is for the P value to compensate the natural cooling of the coffee (a change in temp of 0°C). 

Coffee cooling graphs for different values of P.

A low P won't be able to hold up the temperature. A high P will overshoot and increase in temp. 

Bang-Bang Control
Bang-bang control is a very common approach for thermostats. Why is bang-bang control appropriate for many thermal systems? When might it be insufficient?

Then we used Bang-Bang control to heat the coffee to 375K. We added thermal energy until the coffee reached 375 (or a tiny bit higher) and we turn off the heat. It keeps zig-zagging up and down as a real thermostat would. Even thought we have a range of temperatures, the coffee stays near its target temp. In a different context where the temperature would need to be constant, bang-bang control would not be sufficient- proportional control would be needed.

Proportional Control
How does this approach compare to bang-bang control?

Here we have added proportional control equations: 

error = T - 357 (temp - target)

P[ower] = error *gain

If T is less than target, the power is added. If T is greater than target, P = 0.  
 This graph has a sharper incline and reached the target quicker and is smoother rather than bumpy. 

mfiles:
https://drive.google.com/folderview?id=0B450xdb5jDgEQjVERjBvakdvRlE&usp=sharing&tid=0B450xdb5jDgEWWhwcDN0eUpTSEU